[실전 머신러닝] 선형 회귀 : 보험료 예측하기 ❹

선형 회귀(Linear Regression)는 머신러닝 기초 알고리즘입니다. 복잡한 알고리즘에 비해서는 예측력이 떨어지지만 데이터 특성이 복잡하지 않을때는 쉽고 빠른 예측이 가능하기 때문에 많이 사용됩니다. 다른 모델과의 성능을 비교하는 베이스라인으로 사용하기도 합니다.

이번에는 선형 회귀 모델로 보험 데이터셋을 학습해 보험료를 예측하고, 선형 회귀의 작동 원리를 이해합니다. 총 4편으로 준비했습니다. 총 4편으로 준비했습니다. 4편은 선형 회귀 이해하기입니다.

선형 회귀 이해하기

선형 회귀(Linear Regression)는 독립변수와 종속변수 간에 선형 관계가 있음을 가정하여 최적의 선을 그려서 예측하는 방법입니다. 흔히 선형 관계가 있을 것이라 예측할 만한 예로 키와 체중을 들 수 있습니다. 같은 키라도 사람마다 체중은 천차만별이겠지만, 평균적으로보면 키가 크면 큰만큼 평균 체중 또한 더 많이 나갈 겁니다. 다음 그래프와 같은 데이터가 있다고 가정해 봅시다.

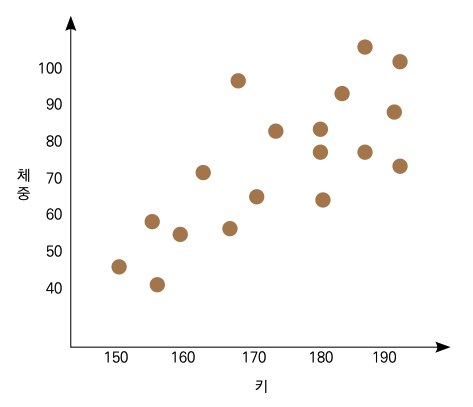
키와 체중이 완벽하게 정비례하지는 않지만, 얼추 선형 관계를 보이는 듯한 분포입니다. 선형 회귀는 여기에 최적의 선을 찾아 그어서 예측하는 겁니다. 그런데 다음 중 어떤 선이 더 최적의 선일까요?

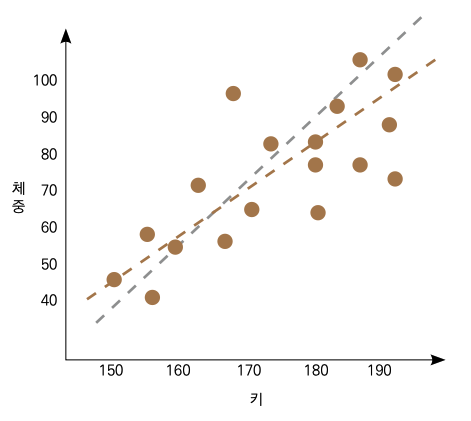
이 부분은 사람의 눈으로 알기가 어렵습니다만, 머신러닝에서는 손실 함수(Loss Function)를 최소화하는 선을 찾아서 모델을 만들어냅니다. 여기서 손실 함수란 예측값과 실젯값의 차이, 즉 오차를 평가하는 방법을 말합니다. 위 그래프에서는 선과 각 점 간의 거리가 오차가 되고, 우리가 앞서 배웠던 MSE나 RMSE 등이 손실 함수가 됩니다. 예측한 선의 기울기나 y절편에 따라서 실젯값과 예측값의 차이가 달라집니다. 머신 러닝은 이 손실 함수를 최소화하는 방향으로 최적의 선을 단시간에 찾아냅니다.

예를 들어 키를 독립변수로 두고, 체중을 종속변수로 하는 선형 회귀를 만들고 다음과 같은 그림의 결과를 얻었다고 가정하겠습니다.

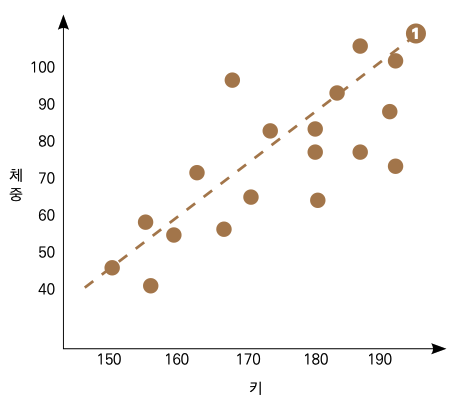
여기서 ❶번 점선이 우리의 예측 모델이 되는 겁니다. 이. 모델을 가지고 새로운 데이터를 예측한다면 다음과 같이 설명할 수 있습니다. 예를 들어 키가 170인 새로운 사람에 대한 체중을 예측한다면 ❷번 점선에서 보이는 것처럼 해당 키에 해당하는 체중값으로 약 72kg 정도의 예측값을 보여줄 겁니다.

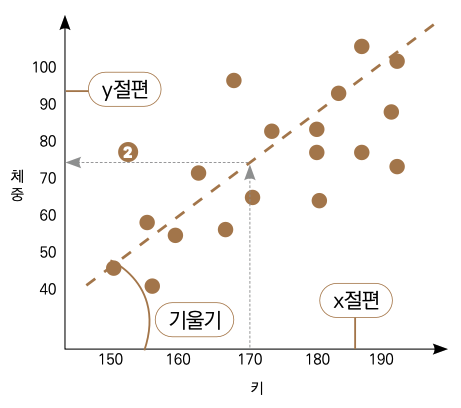
선형 회귀는 상대적으로 단순한 알고리즘이기 때문에 수식으로 표현하기도 쉽습니다. 기초교육과정에서 배운 1차 함수로 표현할 수 있습니다.

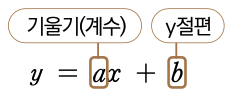
여기서 x는 키, y는 체중이 되며 a는 예측 모델(점선)의 기울기, b는 점선의 y절편입니다. 따라서 x에 170이라는 숫자를 넣으면 약 72 정도의 y값이 나오는 1차 함수인 셈입니다.

이 예시는 독립변수가 ‘키’ 단 한 개뿐이라서 그리기도 쉽고 이해하도 쉽습니다. 우리는 코딩 파트에서 독립변수가 ‘age’, ‘sex’, ‘bmi’, ‘children’, ‘smoker’로 5개인 모델을 만들었습니다. 독립변수가 많아지게 되면 현실적으로 그림으로 표현해 보여주기가 어렵습니다. 하지만 적어도 수식으로는 표현할 수 있으며, 다음과 같은 형태의 수식을 생각해볼 수 있습니다.

여기에서는 y절편을 b 대신 iintercept로 표시해주었고, A, B, C, D, E는 각 변수에 대한 기울기입니다. 이 기울기 값을 계수coefficient라고도 합니다. 사이킷런의 선형 회귀 모델은 예측뿐만 아니라, 학습을 통해 생성된 계수 또한 제공해줍니다.

다음 코드를 실행하면 다음과 같이 독립변수 5개에 대한 계수를 볼 수 있습니다.

model.coef_

array([2.64799803e+02, 1.73446608e+01, 2.97514806e+02, 4.69339602e+02,
2.34692802e+04])

넘파이 형태로 출력되기 때문에 변수의 이름이 따로 나타나지 않는데, 기존 데이터의 독립변수와 같은 순서로 배열되어 있습니다. 더 보기 편하도록 변수 이름을 포함하는 판다스 형태로 변경하겠습니다. 한 줄짜리 데이터이므로 시리즈 형태로 바꿔보겠습니다.

pd.Series(model.coef_, index = X.columns)

age 264.799803
sex 17.344661
bmi 297.514806
children 469.339602
smoker 23469.280173
dtype: float64

변수 이름이 함께 나오니 훨씬 해석이 용이해졌습니다. 몇 가지 변수를 해석하자면, age가 1만큼 증가하면 charges는 약 265만큼 증가합니다. sex는 0과 1로만 구성된 데이터이기 때문에 ‘1만큼 증가할 때 charges가 17만큼 증가한다기’보다는, ‘남자(1)의 경우 여자(0)보다 charges가 보통 17정도 높다’고 해석하는 게 좋습니다. smoker도 sex와 마찬가지로 해석할 수 있습니다.

학습된 모델은 계수뿐만 아니라 y절편 또한 제공해줍니다.

model.intercept_

-11576.999976112367

그럼 위의 정보를 이용해 앞서 언급했던 수식을 제대로 완성하겠습니다.

charges=264.799803_age+17.344661_sex+297.514806_bmi +469.339602_children+23469.280173_smoker-11576.999976112367

데이터의 특정 행을 정해서 각 변수의 값을 위 수식에 넣으면 모델이 보여주는 예측값과 같은 결과를 얻으실 수 있습니다. 이처럼 선형 회귀는 수식을 도출하기 매우 쉽기 때문에 그 해석도 매우 직관적이라는 장점이 있습니다.

학습 마무리

보험 데이터셋을 이용하여 보험사에서 청구할 보험료를 예측하는 모델을 만들어보았습니다. 이 과정을 되짚어보겠습니다.

되짚어보기

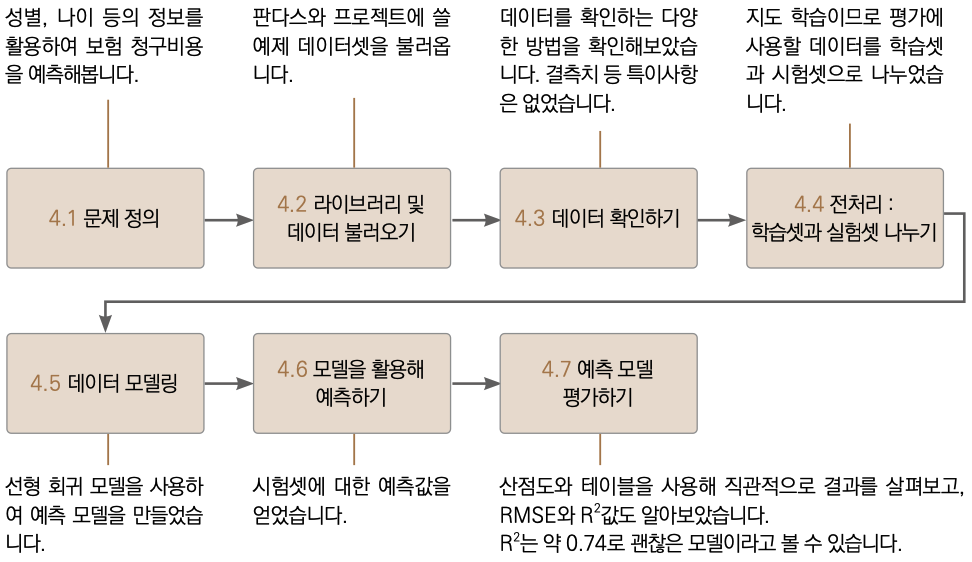
유의할 점

모델의 계수를 해석할 때 부호의 영향에 유의해야 합니다. 부호와 상관없이 계수의 절댓값이 클수록 영향이 크다고 할 수 있고, 절댓값이 0에 가까울수록 영향력이 거의 없는 겁니다. 다만, 여러 계수를 서로 비교할 때 단순히 절댓값이 더 크면 영향력이 더 크다고 보기에는 무리가 있습니다. 이유는 각 변수의 스케일이 다르기 때문입니다. 예를 들어 성별은 0과 1로만 되어 있는 반면 나이는 20부터 60 등 십의 자리 숫자를 가지고 있습니다. 즉, 성별이 1 커질 때와 나이가 1커질 때가 가지는 영향력이 다르다는 겁니다. 이 부분을 명료하게 비교하려면 스케일링 작업이 필요하며, 이는 6장 ‘K-최근접 이웃(KNN)’에서 다룹니다.

관련 모델 안내

1. 릿지 회귀(Ridge Regression)

패키지:

from sklearn.linear_model import Ridge

선형 회귀 모델에 L2 정규화1 를 적용한 모델로 오버피팅을 억제하는 효과가 있습니다.

2. 라쏘 회귀(Lasso Regression)

패키지

from sklearn.linear_model import Lasso

선형 회귀 모델에 L1 정규화를 적용한 모델로 피처 셀렉션 ****및 오버피팅을 억제하는 효과가 있습니다.

3. 엘라스틱 넷(Elastic Net)

패키지

from sklearn.linear_model import ElasticNet

릿지 회귀와 라쏘 회귀의 단점을 절충시킨 모델입니다.

핵심 용어 정리

1. 선형회귀: 독립변수와 종속변수 간의 선형 관계를 전제로 한 모델입니다. 구현 및 이해가 용이한 장점이 있습니다.

2. Null: 값이 비어있는 것을 뜻합니다. 널값, Null value, 결측치 등으로도 부르며, N/A, NA, NaN 등 다양한 방식으로 표현됩니다. Null값은 비어 있어서 알 수 없는 값이지, 0이 아닌 점에 주의하시기 바랍니다.

3. 사분위수(Quantile) : 사분위수는 데이터를 오름차순으로 정리했을 때 25%, 50%, 75% 위치에서 확인한 값입니다. 예를 들어 100개의 값들이 있다고 하면 가장 낮은 숫자부터 하나씩 세어 25번째 데이터, 50번째 데이터, 75번째 데이터가 각각 사분위수 25%, 50%, 75%에 해당합니다. Q1, Q2, Q3라고도 표현합니다.

4. 오버피팅 : 모델이 학습셋에 지나치게 잘 맞도록 학습되어서 새로운 데이터에 대한 예측력이 떨어지는 현상을 의미합니다. 8장에서 더 자세하게 다룰 예정입니다.